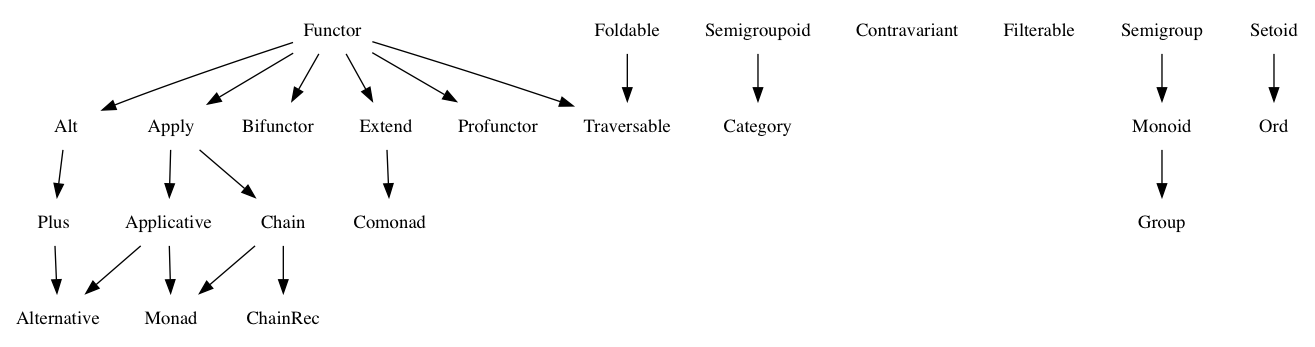
Я все еще знаком со всеми вещами теории этой категории, и почти каждый пример, который я вижу, связан с Maybe или Array. Но я не нашел примеров различий между этими категориями. Например, вот некоторые из вопросов, на которые я все еще не мог ответить:
- Что такое полугруппа, которая не является также моноидом?
- Что такое Складная, которая также не является Traversable? [Дублировать]
- Что такое Functor, который не является также Apply?
- Что такое Apply, которое также не является аппликативным?
- Что такое приложение, которое также не является цепочкой?
- Какова Цепочка, которая не является также Монадой?
- Какая аппликация, которая также не является монадой? [Дублировать]
Я изучаю этот материал в контексте JavaScript FantasyLand, так что, откуда я получаю сообщение, я понимаю это разные слова для этих вещей.