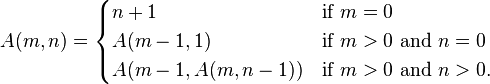Насколько я знаю, большинство рекурсивных функций можно переписать с помощью циклов. Некоторые, возможно, сложнее других, но большинство из них можно переписать.
В каких условиях становится невозможным переписать рекурсивную функцию с использованием цикла (если такие условия существуют)?
Когда вы используете функцию рекурсивно, компилятор позаботится об управлении стеком для вас, что и делает рекурсию возможной. Все, что вы можете сделать рекурсивно, вы можете сделать, управляя стеком самостоятельно (для косвенной рекурсии вам просто нужно убедиться, что ваши разные функции разделяют этот стек).
Итак, нет, ничего не может быть сделано с рекурсией, и это невозможно сделать с помощью цикла и стека.
Любая рекурсивная функция может быть сделана для итерации (в цикл), но вам нужно использовать стек для сохранения состояния.
Обычно хвостовая рекурсия легко конвертируется в цикл:
A(x) {
if x<0 return 0;
return something(x) + A(x-1)
}
Можно перевести на:
A(x) {
temp = 0;
for i in 0..x {
temp = temp + something(i);
}
return temp;
}
Другие виды рекурсии, которые можно перевести в рекурсию хвоста, также легко изменить. Другие требуют больше работы.
Следующее:
treeSum(tree) {
if tree=nil then 0
else tree.value + treeSum(tree.left) + treeSum(tree.right);
}
Не так просто перевести. Вы можете удалить одну часть рекурсии, но другая невозможна без структуры для сохранения состояния.
treeSum(tree) {
walk = tree;
temp = 0;
while walk != nil {
temp = temp + walk.value + treeSum(walk.right);
walk = walk.left;
}
}
Каждая рекурсивная функция может быть реализована с помощью одного цикла.
Подумайте, что делает процессор, он выполняет команды в одном цикле.
Я не знаю примеров, в которых рекурсивные функции не могут быть преобразованы в итеративную версию, но непрактичными или крайне неэффективными примерами являются:
обход дерева
быстрый Фурье
quicksorts (и некоторые другие iirc)
В принципе, все, где вам нужно начинать отслеживать безграничные потенциальные состояния.
Это не так, что они не могут быть реализованы с использованием циклов, это тот факт, что способ, которым работает рекурсивный алгоритм, намного яснее и более кратким (и во многих случаях математически доказуемым), что функция верна.
Многие рекурсивные функции могут быть записаны как рекурсивные хвостовые петли, которые могут быть оптимизированы для цикла, но это зависит как от алгоритма, так и от используемого языка.
Все они могут быть записаны как итеративный цикл (но некоторым может понадобиться стек, чтобы сохранить предыдущее состояние для последующих итераций).
Одним из примеров, которые было бы чрезвычайно сложно преобразовать из рекурсивного в итеративный, была бы функция Ackermann.
Косвенная рекурсия все еще возможна для преобразования в нерекурсивный цикл; просто начните с одной из функций и вставьте вызовы другим, пока не получите прямо рекурсивную функцию, которая затем может быть переведена в цикл, который использует структуру стека.
В SICP авторы заставляют читателя придумать чисто итерационный метод реализации проблемы "счетного изменения" (вот пример один из Project Euler).
Но строгий ответ на ваш вопрос уже задан - петли и стеки могут реализовать любую рекурсию.
Вы всегда можете использовать цикл, но вам может потребоваться создать дополнительную структуру данных (например, имитировать стек).
Косвенная рекурсия приходит в голову...
Изменить: Mile answer показывает, как встроить косвенную рекурсию, поэтому я ошибся.