Как рассчитать коэффициенты полинома с использованием интерполяции Лагранжа

Мне нужно вычислить коэффициенты полинома, используя Lagrange интерполяционный многочлен, как моя домашняя работа, я решил сделать это в Javascript.

- это определение многочлена Лагранжа (L (x))

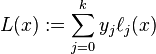
enter image description here

Лагранжевы базисные полиномы определяются следующим образом:

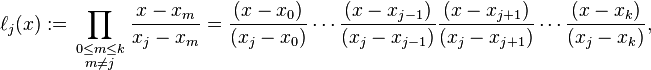
enter image description here

Вычислить значение y для конкретной функции X (W (x)) просто, но мне нужно рассчитать коэффициенты полинома (массив из [a0, a1,..., an]). Мне нужно сделать это с n <= 10, но будет хорошо иметь произвольное n, тогда я могу поместить эту функцию в функцию horner и нарисовать этот многочлен.

enter image description here

У меня есть функция, которая вычисляет знаменатель в первом уравнении

function denominator(i, points) {
   var result = 1;
   var x_i = points[i].x;
   for (var j=points.length; j--;) {
      if (i != j) {
        result *= x_i - points[j].x;
      }
   }
   return result;
}

и функцию, возвращающую y с помощью метода horner (у меня также есть функция рисования с использованием холста)

function horner(array, x_scale, y_scale) {
   function recur(x, i, array) {
      if (i == 0) {
         return x*array[0];
      } else {
         return array[i] + x*recur(x, --i, array);
      }
   }
   return function(x) {
      return recur(x*x_scale, array.length-1, array)*y_scale;
   };
}

кто-нибудь знает алгоритм для этого, или идею, как вычислить эти коэффициенты

ОТВЕТЫ

Ответ 1

Хорошо, вы можете сделать это наивно. Представьте полином массив его коэффициентов, массив

[a_0,a_1,...,a_n]

соответствует a_0 + a_1*X + ... + a_n*X^n. Я плохо разбираюсь в JavaScript, поэтому псевдокод должен будет делать:

interpolation_polynomial(i,points)
    coefficients = [1/denominator(i,points)]
    for k = 0 to points.length-1
        if k == i
            next k
        new_coefficients = [0,0,...,0] // length k+2 if k < i, k+1 if k > i
        if k < i
            m = k
        else
            m = k-1
        for j = m downto 0
            new_coefficients[j+1] += coefficients[j]
            new_coefficients[j] -= points[k]*coefficients[j]
        coefficients = new_coefficients
    return coefficients

Начните с постоянного полинома 1/((x_1-x_0)* ... *(x_i-x_{i-1})*(x_i-x_{i+1})*...*(x_i-x_n)) и умножьте его на X - x_k для всех k != i. Таким образом, это дает коэффициенты для L i, тогда вы просто умножаете их на y i (вы можете сделать это, инициализируя coefficients до y_i/denominator(i,points), если вы передадите y -значения как параметры) и, наконец, добавить все коэффициенты.

polynomial = [0,0,...,0] // points.length entries
for i = 0 to points.length-1
    coefficients = interpolation_polynomial(i,points)
    for k = 0 to points.length-1
        polynomial[k] += y[i]*coefficients[k]

Вычисление каждого L i равно O (n²), поэтому общий расчет равен O (n³).

Обновление: В jsFiddle у вас была ошибка в цикле многочлена умножения в дополнение к (исправленной) ошибке с начальным индексом, который я сделал, это должно быть

for (var j= (k < i) ? (k+1) : k; j--;) {
     new_coefficients[j+1] += coefficients[j];
     new_coefficients[j] -= points[k].x*coefficients[j];
}

Поскольку вы уменьшаете j при тестировании, ему нужно начинать один выше.

Это еще не дает правильной интерполяции, но, по крайней мере, более разумно, чем раньше.

Кроме того, в вашей horner функции

function horner(array, x_scale, y_scale) {
   function recur(x, i, array) {
      if (i == 0) {
         return x*array[0];
      } else {
         return array[i] + x*recur(x, --i, array);
      }
   }
   return function(x) {
      return recur(x*x_scale, array.length-1, array)*y_scale;
   };
}

вы умножаете самый высокий коэффициент дважды с x, он должен быть

if (i == 0) {
    return array[0];
}

вместо этого. Тем не менее, никакого хорошего результата.

Обновление2: Окончательные исправления опечаток, следующие работы:

function horner(array, x_scale, y_scale) {
   function recur(x, i, array) {
      if (i == 0) {
         return array[0];
      } else {
         return array[i] + x*recur(x, --i, array);
      }
   }
   return function(x) {
      return recur(x*x_scale, array.length-1, array)*y_scale;
   };
}

// initialize array
function zeros(n) {
   var array = new Array(n);
   for (var i=n; i--;) {
     array[i] = 0;
   }
   return array;
}

function denominator(i, points) {
   var result = 1;
   var x_i = points[i].x;
   for (var j=points.length; j--;) {
      if (i != j) {
        result *= x_i - points[j].x;
      }
   }
    console.log(result);
   return result;
}

// calculate coefficients for Li polynomial
function interpolation_polynomial(i, points) {
   var coefficients = zeros(points.length);
    // alert("Denominator " + i + ": " + denominator(i,points));
   coefficients[0] = 1/denominator(i,points);
    console.log(coefficients[0]);
    //new Array(points.length);
   /*for (var s=points.length; s--;) {
      coefficients[s] = 1/denominator(i,points);
   }*/
   var new_coefficients;

   for (var k = 0; k<points.length; k++) {
      if (k == i) {
        continue;
      }
      new_coefficients = zeros(points.length);
       for (var j= (k < i) ? k+1 : k; j--;) {
         new_coefficients[j+1] += coefficients[j];
         new_coefficients[j] -= points[k].x*coefficients[j];
      }   
      coefficients = new_coefficients;
   }
   console.log(coefficients);
   return coefficients;
}

// calculate coefficients of polynomial
function Lagrange(points) {
   var polynomial = zeros(points.length);
   var coefficients;
   for (var i=0; i<points.length; ++i) {
     coefficients = interpolation_polynomial(i, points);
     //console.log(coefficients);
     for (var k=0; k<points.length; ++k) {
       // console.log(points[k].y*coefficients[k]);
        polynomial[k] += points[i].y*coefficients[k];
     }
   }
   return polynomial;
}