Вычисление k-core графика путем итеративной обрезки вершин достаточно просто. Тем не менее, для моего приложения я хотел бы иметь возможность добавлять вершины к стартовому графику и получать обновленное ядро без необходимости пересчитывать все k-ядро с нуля. Есть ли надежный алгоритм, который может использовать работу, выполненную в предыдущих итерациях?
Для любопытных k-ядро используется в качестве этапа предварительной обработки в алгоритме поиска клики. Любые клики размером 5 гарантированы как часть 4-ядро графа. В моем наборе данных 4-ядро намного меньше, чем весь график, так что грубая задержка его оттуда может быть приемлемой. Поэтапное добавление вершин позволяет алгоритму работать с максимально возможным набором данных. Мой набор вершин бесконечен и упорядочен (простые числа), но я забочусь только о самой низкой пронумерованной клике.
Edit:
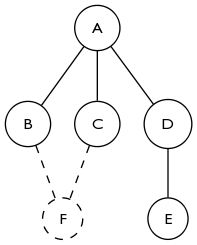
Размышляя об этом еще немного, основанном на ответе akappa, обнаружение создания цикла действительно критично. На приведенном ниже графике 2-ядро пустое до добавления F. Добавление F не меняет степень A, но все равно добавляет A к 2-ядерному ядру. Легко расширить это, чтобы увидеть, как закрытие цикла любого размера приведет к тому, что все вершины будут одновременно присоединяться к 2-ядерному.
Добавление вершины может влиять на coreness вершин на любом расстоянии, но, возможно, это слишком сильно фокусируется на худшем случае.