insertion_procedure (int a[], int p [], int N)
{
int i,j,k;
for (i=0; i<=N; i++) p[i] = i;
for (i=2; i<=N; i++)
{
k = p[i];
j = 1;
while (a[p[j-1]] > a[k]) {p[j] = p[j-1]; j--}
p[j] = k;
}
}
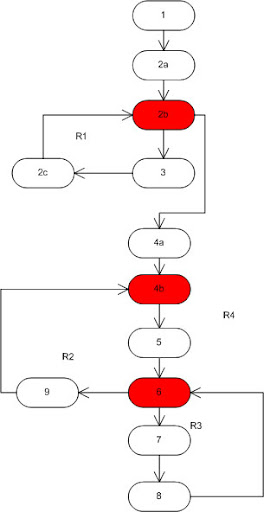
Мне нужно найти цикломатическую сложность для этого кода, а затем предложить несколько тестовых ящиков с белым ящиком и тестовые примеры с черным ящиком. Но у меня возникли проблемы с созданием CFG для кода.
Поблагодарили бы за помощь в тестовых случаях.