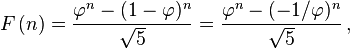Я знаю, как составить список номеров Fibonacci, но я не знаю, как я могу проверить, принадлежит ли данный номер списку фибоначчи - один из способов, который приходит в голову, - это создать список фидов. номера до этого числа и посмотреть, принадлежит ли он массиву, но должен быть другой, более простой и быстрый метод.
Любые идеи?