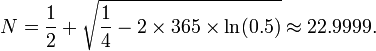Для списка из 10 ints есть 10! возможных порядков или перестановок. Почему random.shuffle дает дубликаты после 5000 попыток?
>>> L = range(10)
>>> rL = list()
>>> for i in range(5000):
... random.shuffle(L)
... rL.append(L[:])
...
>>> rL = [tuple(e) for e in rL]
>>> len(set(rL))
4997
>>> for i,t in enumerate(rL):
... if rL.count(t) > 1:
... print i,t
...
102 (7, 5, 2, 4, 0, 6, 9, 3, 1, 8)
258 (1, 4, 0, 2, 7, 3, 5, 9, 6, 8)
892 (1, 4, 0, 2, 7, 3, 5, 9, 6, 8)
2878 (7, 5, 2, 4, 0, 6, 9, 3, 1, 8)
4123 (5, 8, 0, 1, 7, 3, 2, 4, 6, 9)
4633 (5, 8, 0, 1, 7, 3, 2, 4, 6, 9)
>>> 10*9*8*7*6*5*4*3*2
3628800
>>> 2**19937 - 1
431542479738816264805523551633791983905393 [snip]
>>> L = list()
>>> for i in range(5000):
... L.append(random.choice(xrange(3628800)))
...
>>> len(set(L))
4997
Изменить: FWIW, если вероятность того, что две одинаковые для одной пары не равны: p = (10! - 1)/10! и количество комбинаций: C = 5000!/4998! * 2!= 5000 * 4999/2 то вероятность наличия дубликата:
>>> import math
>>> f = math.factorial(10)
>>> p = 1.0*(f-1)/f
>>> C = 5000.0*4999/2
>>> 1 - p**C
0.96806256495611798